日野弥生:勉強しよう
LeetCode 142 - 环形链表 II
发表于2025年01月14日
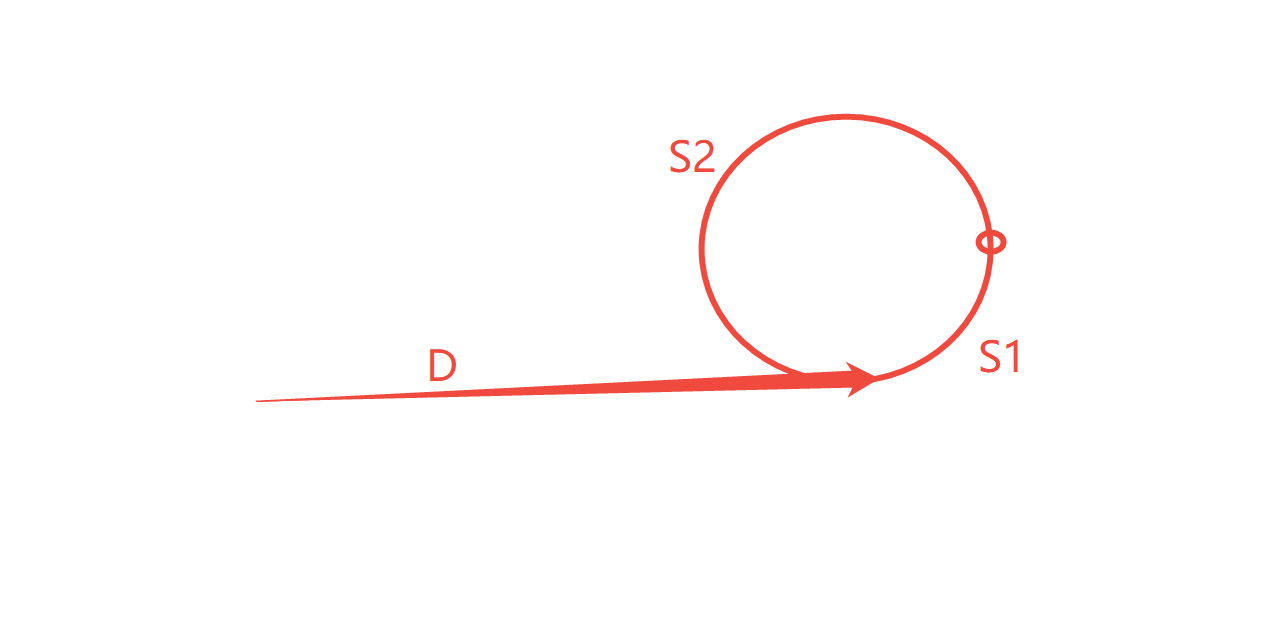
我们需要找到一个环形链表的入环点。 如图所示,假设从链表头节点到环入口点的距离是 D,从入口点到首个相遇点的距离是S1,环的剩余部分长度是 S2。
当两个指针首次相遇时:
指针 P1 每次前进 1 步,总共走过的距离为$D + S1$; 指针 P2 每次前进 2 步,总共走过的距离为$D + S1 + n(S1 + S2)$; 其中 n 为绕环的圈数。
由于 P2 的速度是 P1 的两倍,因此有: $2(D+S1)=D+S1+n(S1+S2);$ 整理得: $D=(n−1)(S1+S2)+S2。$
这表明,从链表头开始走 D 的距离,恰好等于从首次相遇点绕环$(n-1)$圈再回到入环点的距离。 这样一来,只要把其中一个指针放回到头节点位置,另一个指针保持在首次相遇点,两个指针都是每次向前走1步。那么,它们最终相遇的节点,就是入环节点。
class Solution {
public:
ListNode *detectCycle(ListNode *head) {
ListNode *slow = head, *fast = head;
while (fast && fast->next) {
slow = slow->next;
fast = fast->next->next;
if (slow == fast)
break;
}
//判断是否有环
if(fast==nullptr||fast->next==nullptr)
return nullptr;
//有环则将fast移动至head并移动S2距离
fast=head;
while(fast!=slow){
slow=slow->next;
fast=fast->next;
}
return fast;
}
};